The FP of H.P. Lovecraft
-
Forum Statistics
352.3k
Total Topics4.6m
Total Posts -
Member Statistics
125,524
Total Members2,359
Most OnlineNewest Member
Pandit Sahil Sharma Ji
Joined -
Images
-
Albums
-
Ne
- By Penguincollector,
- 0
- 0
- 6
-
pen repair
- By lionelc,
- 0
- 0
- 1
-
March- April -2024
- By yazeh,
- 0
- 0
- 52
-
Misfit’s 4th album of Pens etc
- By Misfit,
- 99
-
Mercian’s Miscellany
- By Mercian,
- 0
- 14
- 22
-
















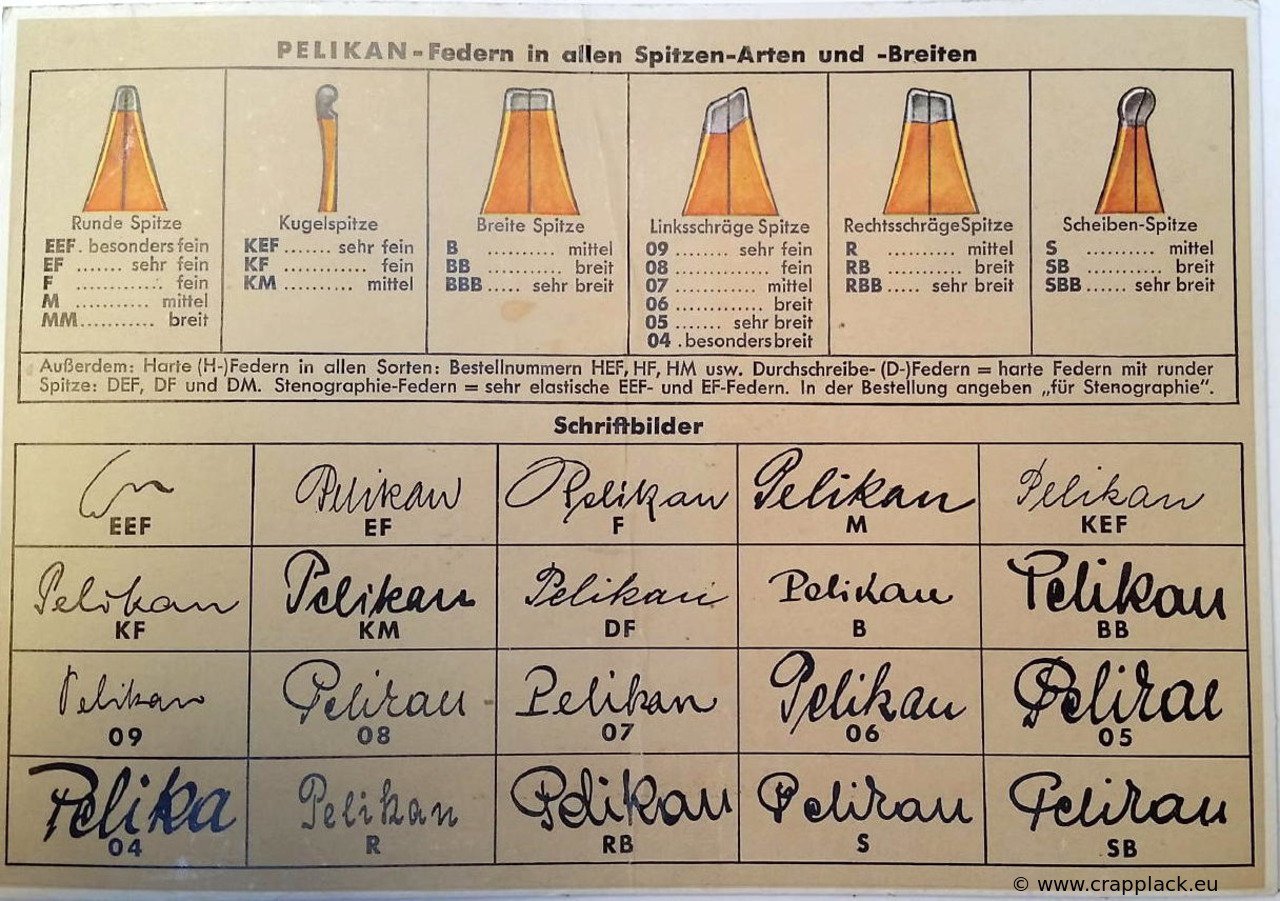

.thumb.jpg.f07fa8de82f3c2bce9737ae64fbca314.jpg)



desaturated.thumb.gif.5cb70ef1e977aa313d11eea3616aba7d.gif)





Recommended Posts
Create an account or sign in to comment
You need to be a member in order to leave a comment
Create an account
Sign up for a new account in our community. It's easy!
Register a new accountSign in
Already have an account? Sign in here.
Sign In Now